Backburner Month 11: Palladio
This is an entry from a list of projects I hope to some day finish. Return to the backburnered projects index.
What is it? An authoring tool for simplistic shape grammars intended for generative art.
A shape grammar is a tool for building two-dimensional objects. Like all grammars, you can think of a shape grammar as either a recognizer of a language or as a generator of a language, and for our purposes it makes more sense to think of them in the latter sense. Also like other grammars, it consists of a set of rules, each of which has a left-hand side and a right-hand side: generating a language from a grammar is a process of finding rules whose left-hand side matches some part of an intermediate state, and then replacing that part with whatever is specified by the right-hand side. Similarly, some components are considered 'non-terminals', which are symbols that always appear on the left-hand side of rules and are meant to be replaced, while others are 'terminals' which form the final output: once a state contains no non-terminals, we can say it has been fully generated by the grammar.
The biggest distinction between a shape grammar and a traditional grammar, then, is that a shape grammar operates over, well, shapes. In the case of Palladio, the intention was for it to operate over sprites on a square grid. As an example, consider a grammar defined by these three rules:
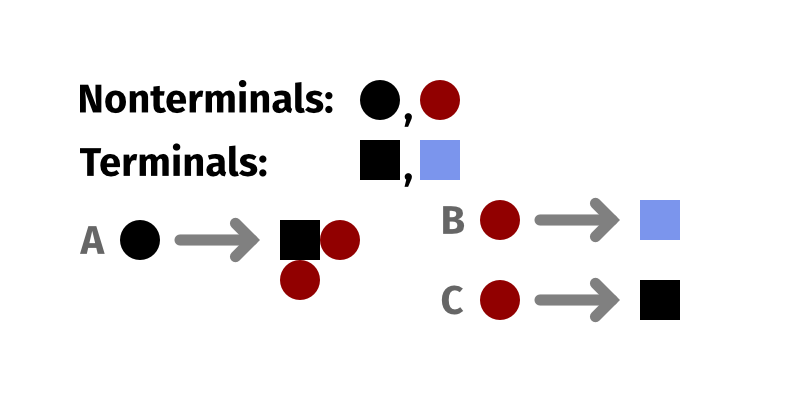
These rules are very simple: when we see a symbol on the left of an arrow, it means we try to find that symbol and replace it with whatever is on the right-hand side. That means if we see a black circle, we replace it with the symbols on the right: in this case, a specific configuration of a black square and two red circles. Similarly, when we see a red circle, we can choose one of the two possible rules that applies here: either we can replace it with a black square, or we can replace it with a light blue square.
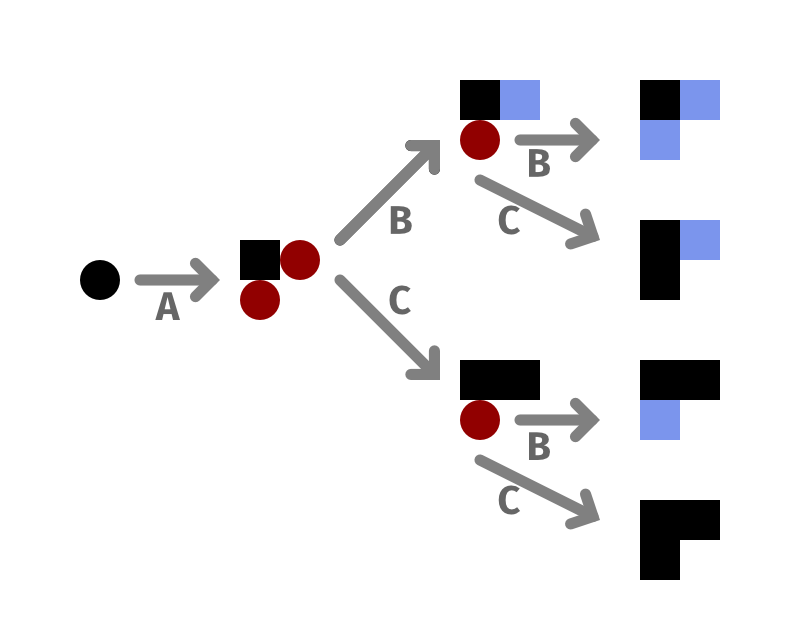
This grammar is non-deterministic, but generates a very small number of possible outputs: rule A will produce one terminal and two non-terminals, and we can non-determinstically apply rules B or C to the resulting non-terminals. In fact, here we can show all four possible outputs along with the rules we apply to get them:
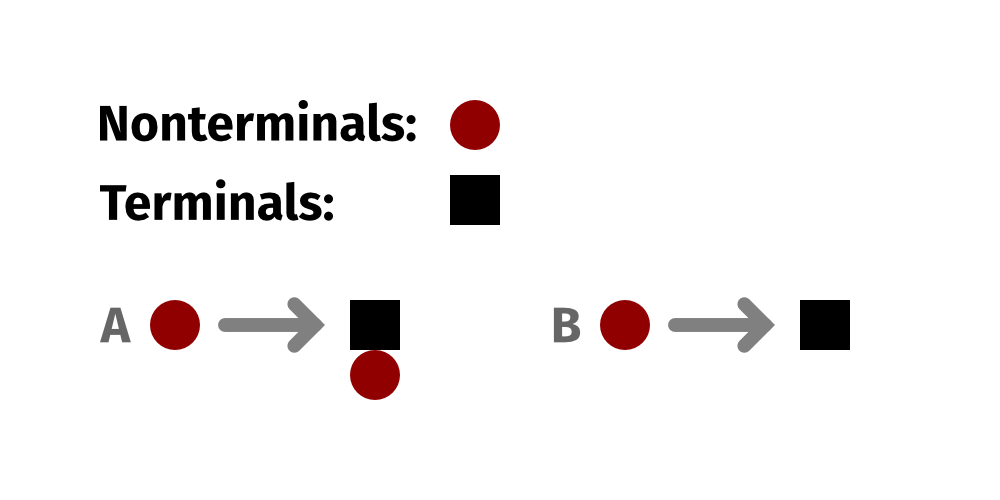
That said, it's not hard to write grammars which produce infinite numbers of possible outputs. This grammar is not terribly interesting, but it does produce an infinite number of possible outputs: in particular, it produces an infinite number of vertical stacks of black squares.
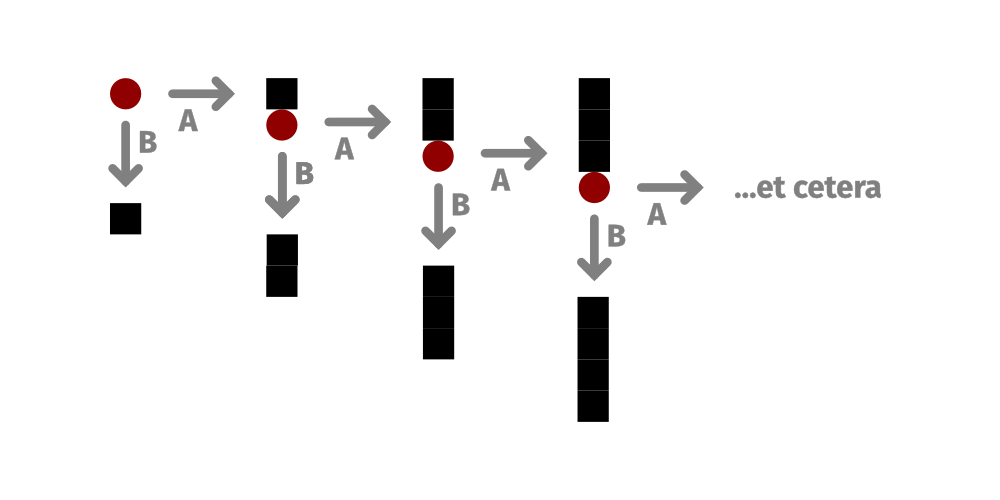
We can't enumerate every possible output here, but you get the idea:
My goal with Palladio was to write an authoring environment for grammars like these, with the specific intention of using them to produce tile-based pixel art pieces. This means not just providing the ability to create and edit rules like these, but with things like live outputs—possibly with a fixed random seed, for stability, and possibly with a large set of seeds, to see wide varieties—and maybe analysis of the output, alongside the ability to export specific results but also the data used to create these.
Why write it? For fun and experimentation! I don't just love making art, I love making tools that make art, and my favorite way to do so is using grammars. Grammars act like tiny constrained programs over some value domain, and you can still bring a very human touch to writing a grammar that produces a specific kind of output.
Doing a tool to support this that's both graphical and constrained to grids is a good way to make it easy to get started with. My plan was even to build tools to spin up Twitter bots as quickly as possible, too, so someone could design a grammar and then with minimal fuss start showing off the output of that grammar on the internet.
My original version (which I admittedly didn't get terribly far with) was written as a desktop app (in Rust and GTK) but I suspect that for the purposes of making it easy to use I'd probably reimplement it to have a web-based version as well, making it easy to open on any device. It'd be nice to also build simple-to-use libraries that can ingest the grammars described, as well, so they can be embedded in other applications like video games or art projects.
Why the name? After the architect Andrea Palladio, but specifically because one of the famous early papers about shape grammars in architecture was Stiny & Mitchell's 1979 paper The Palladian Grammar. Palladio was famously schematic in terms of how he designed and constructed houses, so Stiny & Mitchell were able to take those rules and turn them into mechanized rules which can express the set of possible villas that Palladio might have designed. For a more recent and accessible treatment on the subject, you might look at Possible Palladian Villas (Plus a Few Instructively Impossible Ones) by Freedman & Hersey.